Влияние формы диффузора на направленность громкоговорителя.
В свете дискуссии по данному вопросу, хочется восполнить таки некоторые непонятки по данному вопросу. Вот для затравки... Если ошибаюсь - поправьте.
1. Для нааглядности - картинка, на котрой вдоль диаметра поршня излучателя выделена полоска с некоторой шириной и разобита на участки длиною d.
Когда слушатель находится на оси, на расстоянии более чем диаметр излучателя - волны, поступающие к нему от отдельных участков полоски практически пройдут одинаковые пути и будут, следовательно, синфазны. Общее звуковое давление, создаваемое в рассматриваемой точке будет равно арифметической сумме звуковых давлений, развиваемых отдельными участками.
А вот когда точка наблюдения находится в стороне от акустической оси, под углом на том же расстоянии от акустического центра, звуковые лучи от отдельных участков полоски до точки наблюдения будут проходить разные пути. Например, разность хода у 1 и 2 луча составит Dr=d*sinQ
Рассматриваемый на рисунке треугольник является прямоугольным, так как звуковые лучи перпендикулярны фронту волны.
Сдвиг по фазе между 1 и 2 лучами составит: f=kDr=(2p/l)*d*sinQ
Общее давление в точке наблюдения теперь будет равно геометрической сумме давлений, развиваемых отдельными участками полоски....
Из формулы и рисунка видно, что с увеличением угла Q сдвиг по фазе увеличивается, а суммарное давление уменьшается.
Однако сдвиг по фазе зависит и от отношения d/l. На низких частотах d<l. Следовательно и сдвиг по фазе между лучами практически отсутствует. Это говорит о том, что на нижних частотах излучение поршня под любым углом будет одинаковым, т.е. излучатель будет ненаправленным-будет излучаться шаровая волна.
На высоких частотах d>l, отношение d/l>0 и возникнет фазовый сдвиг межу лучами. Этот фазовый сдвиг будет тем больше, чем больше будет отношение d/l. Суммарное звуковое давление при увеличении угла будет уменьшаться и излучатель приобретет направленные свойства. На втором рисунке приведены диаграммы направленности на низких и высоких частотах.
В случае наличия второго конуса, ситуация несколько усложнится. вплоть до частоты f1 %) излучение головки будет практически отсутствовать. Обратная волна, обогнув конус, будет полностью гасить прямую, так как они находятся в противофазе. Сдвиг по фазе за счет дополнительного пути при огибании диффузора Dr близок к нулю, так как Dr<l. Частота f1, на которой происходит первое усиление, соответствует условию Dr=2R=l/2 (R-радиус поршня излучателя). У 75ГДШ-3-3 с диаметром ВЧ диффузора 0,011 м, условие Dr=2R=l/2 будет выполняться при R=l/4. При этом длина волны составит l=4R=0,22 м, а частота = . Следовательно, у такого ВЧ конуса, излучение будет практически отсутствовать вплоть до частоты примерно F1=1700 Гц.
Но все это относительно плоских излучателей.
Кроме того, это без вопроса выхода диффузора изз поршневого режима, отключения секторов и зонального излучения...
1. Как изменяется зависимость если излучатель конусообразный или сферический...
Я так понимаю, тут на частотах, длины которых сопоставимы или меньше чем глубина конуса или еще какие габариты)) появляются дополнительные интерференции между зонами излучения у основания конуса и у его раскрыва. а так же влияние раскрыва самого конуса. Вопрос КАК?
2. Взаимовлияние двух конусных излучателей...
Если основной диффузор в следствие выхода из поршневого режима или больших внутренних потрь, сам заканчивает излучение в области "подключения" ВЧ конуса - то оно понятно, но если нет - то будет еще и взаимовлияние НЧ и ВЧ конусов.
Вот тут нужны всякие фазовыравнивающие кольца "экранирующие" излучение из щели между ВЧ и НЧ конусами.... пули и грибы....
3. Пуля в конусном излучателе - что делает она реально..
Даеш обсуждение с линками... только просьба конструктивнее.
Сообщение от Gajdar
и только в серии 75ГДШ-3-3 был исправлен этот ляп с шифероподобной формообразующей. 
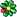
Социальные закладки