
По результатам всех прошедших экспериментов пока получается следующее (это уже ближе к практическому построению усилителя):
1. один излом, даже резкий, на АХ намного менее опасен, чем мелкие осцилляции.
2. Есть область самого неприятного и заметного количества осцилляций. До нее - "подхрипывание", выше нее - "шум".
3. При прочих равных лучше однотактная схема, которая может обеспечить наиболее гладкую АХ. При этом вид ее "кривизны", видимо, не настолько важен. Главное - без колебаний.
4. Лучше однокаскадная схема. Для увеличения усиления лучше стараться параллелить приборы. И по возможности не использовать динамические нагрузки (как ухудшающие монотонность АХ).
В общем, нужно еще проверить экспоненту с вещественным аргументом в качестве АХ и многокаскадное включение (хотя по второму похоже, понятно, что получится..).
Ну и плавно переходить к динамической АХ.
С наилучшими пожеланиями, Евгений.

Добавил по ссылке еще имитацию биполярного транзистора и искажений типа "ступенька".
https://drive.google.com/folderview?...ms&usp=sharing
s_max - максимальная амплитуда сигнала (0,5).
Математика биполяра:
k = 10; % масштабный коэффициент сигнала. "1" означает амплитуду на условном переходе ~26мв
Ucm = 1; % напряжение смещения
% автовычисление вспомогательных величин
Ks = k*26e-3/s_max;
Km = s_max*((exp(s_max*Ks+Ucm) - exp(-s_max*Ks+Ucm))/2)^-1; % нормировка усиления
expcm = exp(Ucm);
[S] = Out_L;
Out_L = Km * (exp(S*Ks+Ucm) - expcm);
[S] = Out_R;
Out_R = Km * (exp(S*Ks+Ucm) - expcm);
файлы out_test_х_sn_exp_1.flac содержит искажения, как если бы на вход транзисторного каскада подавали сигнал амплитудой 26 мВ,
файлы out_test_х_sn_exp_10.flac содержит искажения, как если бы на вход транзисторного каскада подавали сигнал амплитудой 260 мВ.
Математика "ступеньки":
k = 0.05; % уровень ступеньки относительно амплитуды сигнала
% автовычисление вспомогательных величин
th = s_max * k;
[S] = Out_L;
Out_L = S .* (S>=th) + S .* (S<=-th) + (S<th & S>-th) .* (th * sign(S) .* (S/th).^2);
[S] = Out_R;
Out_R = S .* (S>=th) + S .* (S<=-th) + (S<th & S>-th) .* (th * sign(S) .* (S/th).^2);
файл out_test_2_sn_ступенька_0.05.flac содержит искажения при ступеньке высотой 0.05 от максимальной амплитуды сигнала,
файл out_test_2_sn_ступенька_0.1.flac содержит искажения при ступеньке высотой 0.1 от максимальной амплитуды сигнала.
Выводы.
1. Еще раз подтвердилось, что простой каскад на биполяре "рулит".
2. Ступенька весьма заметна (при ступеньке высотой 0.05 уровень максимальной гармоники не превышал -60 дБ !). (ПМСМ, видимо, из-за того, что такие искажения неестественны, а слуховой аппарат это четко определяет).
Теперь с разными видами "негладких" все ясно..
Со статическим искажениями - все.
ЗЫ.
Если рассматривать степень заметности искажений в связи с их возможностью возникновения в естественных условиях, то интересно, как в этом разрезе будут выглядеть "фазовые".
И еще.. Похоже, потеря слабых послезвучий имеет другую причину, чем статическая нелинейность..
Скинул на диск почищенную модельку (файл "Static_nonlinerar_wav_processing.m"). Если кому интересно побаловаться самому.
Upd! В модель добавил автовыравнивание громкости выходного файла и проверил, как работает. Файл обновил.
Последний раз редактировалось bukvarev; 26.04.2015 в 00:32.
С наилучшими пожеланиями, Евгений.
Спасибо, Евгений!
Отслушал девять файлов предыдущей заливки (многоступенчатость). Не знаю (не вдавлся в детали ААХ) чего там Евгений намудрил, буду относиться как к чёрному ящику. От первого ("начало искажений") до 6-го файла искажения на слух нарастают с сохранением общего характера. Затем на седьмом происходит прыжок в сторону. Восьмой файл по характеру искажений больше соответствует предыдущей тенденции и делит с четвёртым первое место по гадости.
Первый файл - на пределе разрешения моей скайп-системы. Типа, шото слышно, может быть тарелки как-то менее благозвучны, и скрипка (вторая часть) чуток визглявее.
Второй - как будто произвели перезапись средненьким таким рекордером. Гитара со смычковым контрабасом начинают взаимодействовать, сцена уплощается.
Третий - чиста эмпэтри с подзвякиванием.
Четвёртый и восьмой - сушите вёсла.
Остальные - катастрофа.
2bukvarev.
По экспоненте (ещё не слушал). При минус бесконечности оно стремится к нулю (Ку=>0). Насколько относительно нуля завышена "рабочая точка" для обоих случаев? Обычно классика жанра |Umax| возбуждения. Т.е. координаты рт в ААХ для обоих случаев. Если координаты не изменились, то ты константу перед экспонентой поменял ("вытянул" её)?
По "ступеньке" (ещё не слушал). Там две. У какой в нуле меньше дифференциальный Ку (производная)?
По "слабым послезвучиям". Многоступенчатость (предыдущий тест) здорово их ест, как мне слышится (уплощается, налезают струны разных инструментов друг на друга, цимбалы (тарелки) бумажно-пластмассовыми становятся)
Последний раз редактировалось Игорь Гапонов; 26.04.2015 в 00:43.
e в первой степени. Теоретики пишут, что от рабочей точки спектр гармонических искажений зависеть не должен. Я сейчас попробовал смещение е в квадрате.. Теоретики правы. В модели смещение задается параметром "Ucm = 1; % напряжение смещения". Для Ucm=1 имеем e в первой степени, для Ucm=2 будет е в квадрате и.т.д.
Ээ.. У той, у которой меньше порог (0.05). Ступеньку представил в виде отрезка параболы, умноженной на знак сэмпла. Т.е. вблизи 0 там все гладко. На границе стыка параболы и линейной части сглаживать не стал. Оставил излом. Таким образом, в ААХ есть два излома и "симметрированная" парабола в центре.
Зы. Но если строго брать производную, то в обоих случаях в нуле она равна 0.
С наилучшими пожеланиями, Евгений.
Совсем не понял. Размах на выходе надо сохранять при изменении рт. Должна расти асимметрия=> Ку=exp(x). Иначе зачем "два" опыта? Можно иначе - коэфф. перед экспонентой поменять.
По ступеньке. А чего в лоб не просуммировал две "зеркальные" экспоненты (для второго случая - другая координата суммирования аргумента)? оно очень даже гладко в рт получается (sh(x))Если симулировать точку перегиба наверное надо как-то поиграть с четырьмя экспонентами с разными показателями, должно очень реально получиться - с ограничением и тремя точками перегиба, одна из них, "центральная", в рт (или специально мимо или гуляет
) .
Последний раз редактировалось Игорь Гапонов; 26.04.2015 в 01:03.
Два опыта - для разных амплитуд сигнала на входе. В этом случае будет разный спектральный состав искажений.
В модели все автонормировано. Все внесенные постоянные смещения вычитаются после нелинейной обработки:
Out = Km * (exp(S*Ks+Ucm) - expcm); где expcm = exp(Ucm) - "смещальщик" постоянной составляющей рабочей точки после нелинейного преобразования, а Кm - как раз нормировщик выходного усиления.
Ну, а exp(S*Ks+Ucm) - это сама "масорубка".
---------- Сообщение добавлено 03.07 ---------- Предыдущее сообщение было 02.58 ----------
Да не знаю даже.. Как рука пошла. (Я ступеньку уж так, "до кучи" решил в последний момент проверить).
В принципе могу сгладить стыки и по sh(x). Стоит заниматься? (а то уже настроился на модуляции).
С наилучшими пожеланиями, Евгений.
1. это эквивалентно изменению коэфф. перед экспонентой. Ясно - принимается.
2. Да как хочешь. Можно у Nick-nack-а спросить, может есть готовая функция. Собственно, с комбинацией экспонент более адекватная модель получается. И в нуле Ку не ноль, это ж не C или "чистый В" режимы
Тут, конечно, я перебрал с уровнями искажений. Сожрут все, что можно.
Но мне очень хочется услышать именно эффект срезания затухания слабых звуков.. Которые я слышал на хорошей акустике. А здесь вроде как все доигрывается, правда, очень "грязно", согласен (ступеньку - не в счет).
---------- Сообщение добавлено 03.17 ---------- Предыдущее сообщение было 03.15 ----------
Бесспорно, да и без грубых стыков.. Результат точно будет почище.
С наилучшими пожеланиями, Евгений.
И "модулировать" их, по-моему, вообще никаких трудностей не должно быть (гладкость будет всегда, лмшь бы в отрицательную проводимость не залазить, хотя...), и даже "по фазе". Типа, для будущих опытов над живыми людьми может пригодиться.
О! Всё должно быть просто - сумма двух th(x) смещённых туда сюда один от другого... Можно даже разные транзисторы в плечах моделировать - th(x) vs th(ax).
По результатам оценки влияния количества "перегибов" ААХ на качества звучания, я решил таки проверить, что же делает с ААХ введение ОООС. Изменяет ли ОООС количество "перегибов" ААХ? Если увеличивает, то понятно - субъективное качество воспроизведения будет улучшаться в меньшей степени, чем глубина ОООС. Если же ОООС не изменяет или уменьшает количество перегибов ААХ, то тогда ее "негативное" влияние на вид ААХ можно исключить.. В последнем случае, если ОООС и может сделать что-то "плохое", то это будет вызвано какими-либо другими следствиями ее работы.
Для проверки написал модель усилителя с изменяемым видом ААХ первого каскада, частотой первого полюса 50 кГц, петлевым усилением 10 и 100% ОООС. В ходе экспериментов менял и усиление, и вид ААХ до охвата ОООС.
На графиках представлены результаты для трех видов ААХ, использованных в предыдущих экспериментах. Первый график - вид ААХ до (синий) и после (красный) введения ОООС. Второй - нормированные колебания ААХ с убранной линейной компонентой (детренд). Графики строились по линейному входному воздействию, но улучшение спектрального состава имеет место и при произвольном воздействии на модель усилителя.
Первая пара графиков - имитатор каскада на биполярном транзисторе (экспонента в ААХ):

Далее - имитация осциллирующей ААХ:
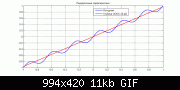
Наконец, сильно искажающая ААХ 7 порядка:
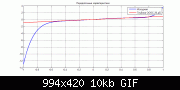
Выводы в части ААХ наглядны.
Ничего плохого пока в ОООС я не увидел, но вот хорошее - есть. ОООС способна восстановить потери в сигнале (заключающиеся в возможной компенсации продуктами искажений сильных сигналов компонентов слабых сигналов), вызванные нелинейностью.
С наилучшими пожеланиями, Евгений.
ОООС уменьшает статическую нелинейность, тут нет никаких сомнений, для этой цели ее и вводят.
---------- Сообщение добавлено 23.45 ---------- Предыдущее сообщение было 23.43 ----------
В плане ОООС интересно ее влияние на динамическую нелинейность, включающую и фазовые проблемы.
Жизнь - это такая Хрень, где-то между Инь и Янь... пена на поверхности океана какой-то иной реальности.
Ээ.. Не так все просто. Введение ОООС изменяет соотношение между спектральными компонентами искажений и добавляет новые.
Это известный факт. Вначале я проверил влияние на звук статических искажений достаточно жесткого вида (out_testх_sn_-27-27-33-41-46-53).
Оказалось, что все не так плохо..
Задачей же последнего эксперимента не было показать, что ОООС уменьшает статическую нелинейность (это очевидно и без исследований),
но проверить, не увеличивает ли введение ОООС количество перегибов ААХ. А это, согласитесь, две большие разницы.
Offтопик:
ЗЫ. Да не волнуйтесь Вы так за фазовые.. И до них доберемся.
С наилучшими пожеланиями, Евгений.
Парочка графиков в дополнение..
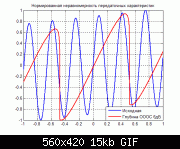
Получены при меньшей глубине ОООС.
Видно, что введение ОООС как бы "растягивает" ААХ первого каскада, и из нее используется только часть.
Кроме того, "плавные" изменения этой ААХ введение ОООС обостряет, расширяя спектр вносимых искажений.
Количество "перегибов" после введения ОООС не может превышать их количество в исходной ААХ, и определяется областью ААХ входного каскада, используемого после охвата ОООС.
В общем, при введении ОООС нужно точно знать, что в используемой области исходная ААХ входного каскада имеет монотонный характер, и все будет хорошо.
Дальше будем начинать эту область "шевелить".
С наилучшими пожеланиями, Евгений.
"Осциллирующая" ААХ все таки является синтетической. Если уменьшить амплитуду колебаний ААХ, чтобы не было участков с отрицательной производной, то условие устойчивости будет выполняться всегда. Также поможет увеличение петлевого усиления.
Что касается пушного зверя, то в данном случае - не придет. Просто будет аналогово-ключевой усилитель.
С наилучшими пожеланиями, Евгений.
Социальные закладки