Offтопик:

Сообщение от
gross

есть текст
У меня идея по поводу Монтан, на которую натолкнули уважаемые коллеги, которые согласились потратить время на
обсуждение интерференции по моей просьбе.
Возможно, многие тут понимают все, но обсуждение интерференции в моей ветке все-таки показало, что не всегда понимание интерференции, как волнового физического явления, бывает глубоким (по моей скромной оценке).
Итак, на 4 кГц длина волны 8,5 см. А сколько звучит одна синусоида на таких частотах, если спектр излучения музыкального сигнала преобразовать Фурье-анализом?
Иными словами, каково характерное время длины одной моды колебаний? Это трудно оценить в теории (для этого не годятся популярные программы, рисующие спектр), но можно узнать в эксперименте.
Вы же понимаете, что этот ответ дает нам ответ на вопрос о том, насколько долго у нас одна мода может сохранять свою когерентность.
Ведь интерферируют только когерентные волны. А если окажется, что разность хода волн до потенциального слушателя будет больше, чем длина каждой такой моды, то интерференции не возникнет - волны будут складываться хаотично.
В квантовой физике есть понятие времени цуга - это время. в течение которого электрон атома переходит с одной орбиты на другую и при этом он излучает фотон (т.е. цуг).
Так вот, при сложении цуга с самим собой (то есть при разделении его на чем-то (на щелях, призмах, линзах), а потом при сложении этих частей на какой-то поверхности), если одна часть цуга прошла расстояние настолько большее, что вторая часть цуга "прилетает" в точку с заметным опозданием, то эти волны не рождают интерференцию - они не складываются.
Это значит, что если до слушателя наши звуковые "цуги" из двух динамиков придут с сильной разбежкой, то интерференции не будет.
Тем не менее, интерференция в этой зоне возникнет на стационарном сигнале (синусе или наборе синусоид).
Но на реальном музыкальном сигнале, в интересующем нас диапазоне частот (то есть 4-5 кГц) каждая мода колебаний может длиться непродолжительное время, например, 2-3 периода. Затем этот "цуг" прекращает существование и возникает другой. возможно даже с той же частотой, но он ничего не знает о фазе предыдущего. Так если "цуги" идут друг за другом, но теряют всякую информацию о фазе предыдущего "цуга" - то в точке их сложения интерференции не будет. Правда в том лишь случае, если разность хода до этой точки будет сравнима с длиной такого "цуга". Я не знаю, может так звучит даже голос человека?
Но если расщепленный цуг будет складываться сам с собой, то несмотря на то, что цуги, испускаемые последовательно, могут терять информацию о фазе друг друга, интерференционная картина все равно будет - каждый цуг будет интерферировать сам на себе (то есть одна его часть, прошедшее одно расстояние будет с складываться с другой, прошедшей другое расстояние). И поскольку эти расстояния фиксированы, то независимо от потере фазы от цуга к цугу - интерференционная картина будет сохраняться, как результат сложения каждого цуга на самом себе, что будет давать всегда один и тот же результат по амплитуде в точке наблюдения.
На картинке я изобразил, как смог, ситуацию, когда в ухо одна часть цуга приходит с сильным запозданием.

:
Видно, что одну часть цуга мы уже почти поглотили ухом, а вторую поглотим вслед за ней. Они могут перекрываться на 10-20%, но никакой интерференции между ними не будет - ведь условие когерентности будет нарушено во времени их прибытия в ухо.
А если цуги будут складываться с какими-то другими (не сами с собой), пусть даже одной или почти одной частоты - фазы их будут хаотичны. поэтому их сложение не чревато провалом в звуковом поле на этой частоте, там где на "длинной" синусоиде был бы провал звука.
Это условие не выполняется, когда динамики у нас стоят друг от друга на расстоянии порядка длины волны (при сведении колонки) - ведь вряд ли длина "цуга" (т.е. звукового фотона) меньше длины волны. Но даже в этом случае при близком расположении источников звука (динамиках) и малых углах (20-30-40 градусов) отклонения от перпендикулярной оси все равно будут систематические (т.е. не единичные) вычитания таких кусков волн, испускаемых разными динамиками.
То есть все дело в систематичности сложения волн, несущих информацию о фазе. Если оно не систематическое - провалов в звуке не будет.
Однако опыты показывают, что даже на розовом шуме интерференционные провалы все-таки образуются, пока отраженный от стен сигнал не забьет прямой по интенсивности. Но в микрофоне он-то забьет, а вот мозг устроен сложнее микрофона (у большинства людей) - мозг дифференцирует инфу от прямого сигнала и уделяет ей больше своих мощностей для анализа.
Можно оценить, какова максимальная разность хода до слушателя от 2-х СЧ динамиков Монтана, играющих около 4 кГц (не синусоиду, а музыку). Это наверное, что-то около 15 см. (Я просто не знаю геометрии этой акустики). А длина волны 8.5 см. Если Цуги перекрываются на половину, то это погасит интерференцию в 2 раза (то есть снизит разницу между интерференционными максимумами звука и минимумами).
Вот весь вопрос тогда в характерной длине "цуга". То есть при разложении в ряд Фурье насколько долго одномодальная синусоида может сохранять свою частоту и непрерывность фазы (то есть оставаться синусоидой) на реальном звуковом материале причем именно на этих частотах (несколько кГц).
Если все изложенное совсем нелепо, тогда прошу меня извинить за этот ОФФ.





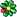
Социальные закладки