Заинтересовала меня недавняя дискуссия в теме «О фазолинейности. Продолжение или революция?!» о погрешности, вносимой конвольвером. После слов ViktKorsя решил проверить, какая же «грязь» может возникать после применения фазового FIR-фильтра.
Пусть у нас есть дискретные отсчёты сигнала с частотой выборки 48 кГц. Построим all-pass фильтр с коротким окном на 16 отсчётов. Постараемся сделать так, чтобы коэффициент передачи по амплитуде был равен 1, а фаза менялась по закону косинуса от частоты. При 0 Гц фаза равна 0°, при 12 кГц – минус 90°, а при 24 кГц достигает минус 180°. Для вычисления 16 искомых коэффициентов конвольвера нам нужно решить систему из 16 линейных. Я зафиксировал 7 точек на шкале частот 3,6,9,12,15,18,21 кГц. Для них по условиям задана фаза и амплитуда, что даёт 14 уравнений. Ещё два уравнения даёт условие для коэффиициента передачи +1 на частоте 0 Гц и минус 1 на частоте 24 кГц. Эти частоты стоят особняком, так как на них фаза может быть либо 0° либо ±180°.
Решаем систему и получаем 16 коэффициентов конвольвера:
Проверяем, строим график ФЧХ и радуемся:Код:0.0000000000000002 0.9722096263235436 -0.0000000000000001 -0.1668931209924746 0.0000000000000001 -0.0025951830757338 -0.0000000000000001 -0.0016313244799198 0.0000000000000001 0.0015642123336106 -0.0000000000000001 0.0070858939842292 0.0000000000000000 0.0288213444185797 -0.0000000000000002 0.1614385514881652
Целевая фаза показана зелёным цветом, а точки аппроксимации синие кружочки.
Но есть один нюанс. Исходный сигнал содержит, конечно, больше частот, чем наши 9 штук прибитых гвоздями с шагом 3 кГц. Эти частоты тоже буду преобразовываться при свёртке с нашим окном из 16 коэффициентов. Их ФЧХ показана красной кривой. Между узлами интерполяции меняется даже знак производной, т.е. часть частот с положительным ГВЗ будут отставать, а другие с отрицательным ГВЗ – наоборот опережать соседей.
На графике АЧХ картина столь же ужасна.
Хотя точки с шагом 3 кГц точно лежат на целевой зелёной полке 0 дБ, но зато между ними мы огребаем погрешность от -4 до +2 дБ.
Первая мысль была: надо взять больше точек и всё улучшится, но расчёты говорят об обратном.
Увеличил в 16 раз длину конвольвера до 256 точек.
Смотрим и видим, что хотя в самих узлах аппроксимации АФЧХ всё волшебно, но между ними творится кошмар. Одни частоты усиливаются, другие ослабляются, а фаза у всех разъехалась в разные стороны от целевой кривой. Причём амплитуда погрешности и не думает уменьшаться с ростом окна.
Есть у меня подозрения, что именно "лохматость" АФЧХ конвольвера воспринимается на слух как "грязь".




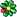


Социальные закладки