Чему пропорционально звуковое давление скорости или ускорению диффузора?

[_Сам_]

Вопрос из заголовка периодически всплывает в обсуждениях темы ЭМОС. Лично мне хочется его прояснить и начну я плясать от этого источника. Хотя там есть вся необходимая информация, но к сожалению нет прямого ответа на вынесенный в заголовок вопрос.

Рассматривается плоский невесомый поршень, совершающий гармонические колебания амплитудой A и циклической частотой ω по закону x(t) = A*cos(ωt), а в комплексной форме x(t) = A*(cos(ωt) + i*sin(ωt)).

Хотя поршень и невесом, но из-за взаимодействия со средой к нему приходится прикладывать конечную силу F(t) = dx/dt * z_R, где z_R - комплексное сопротивление излучению.

Представим сопротивление излучению в виде z_R = ρ*с*S*( r_R + i * x_R ), где ρ - плотность среды, с - скорость звука, S - площадь поршня, а r_R и x_R безразмерные коэффициенты активного и реактивного сопротивления.

Разделив силу F прикладываемую к поршню на его площадь S мы получим создаваемое им звуковое давление
P(t) = F(t) / S = A*ω*( - sin(ωt) + i * cos(ωt) )*ρ*с*( r_R + i * x_R )

Последний шаг: Выделим вещественную часть этого произведения, которая в явном виде описывает закон изменения давления от времени t.
Re(P(t)) = ρ*с*A*ω *( - x_R * cos(ωt) - r_R * sin(ωt) ) = - ρ*с*A*ω*sqrt( (r_R)² + (x_R)² )*cos( ωt - arctg(r_R/x_R) )

Мы получили выражение для амплитуды звукового давления создаваемого колеблющимся поршнем

P_зв = ρ*с*A*ω*sqrt( (r_R)² + (x_R)² )

В коэффициентах r_R и x_R спрятана вся физика взаимодействия поршня со средой. Самое интересное состоит в том, что они зависят от частоты ω. Для поршня в бесконечном экране r_R и x_R изменяются следующим образом:

Здесь аргументом является безразмерный параметр ka = ωa/c, где а - радиус поршня. Для малых значений ka << 1 известны асимптотические зависимости x_R= 8ka/3, r_R = 0.5*(ka)².

Прикинем значение ka для типичного сабового динамика калибра 12 дюймов. Исходя из его примерного радиуса a = 0.125 м параметр ka изменяется от 0 до 0.23 в рабочей полосе частот от 0 до 100 Гц. Значит для него можно использовать приближённые формулы x_R= 8ka/3, r_R = 0.5*(ka)²

Построим график sqrt( (r_R)² + (x_R)² ) и увидим, что при ka < 1 он представляет собой практически прямую линию.

Это означает, что сопротивление излучению линейно растёт с увеличением частоты ω, а поскольку перед корнем уже стоит множитель ω, то мы получаем квадратичную зависимость P_зв от частоты.

Вывод:


1. Поршень с радиусом много меньше, чем длина излучаемой волны создает звуковое давление, которое линейно растёт с увеличением амплитуды колебаний поршня А и по квадрату частоты его колебаний ω. Легко заметить, что линейное ускорение поршня изменяется точно также. d(dx/dt)/dt = -A*ω*ω*cos(ωt) Потому в НЧ области для ЭМОС правильно использовать ускорение диффузора в качестве предсказателя звукового давления.

2. С ростом частоты ситуация меняется. При ka больше 4 множитель sqrt( (r_R)² + (x_R)² ) становится постоянным и в этом случае звуковое давление пропорционально скорости поршня. Для двенашки ka = 2 примерно соответствует частоте 1 кГц. В принципе это хорошо коррелирует с картинкой от Nota Bene.

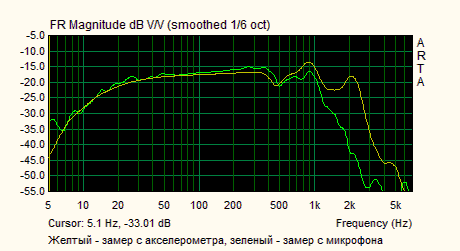
где видно, что с 1 кГц акселерометр даёт завышенное значение относительно измерений микрофона.

[Бока]

у вас до 100гц всё совпадает, а дальше вам зачем сравнивать? дальше как бы уже не бас. дальше длина волны с диаметром диффузора вступают в противоречие

---------- Сообщение добавлено 17:17 ---------- Предыдущее сообщение было 17:16 ----------

у вас до 100гц всё совпадает, а дальше вам зачем сравнивать? дальше как бы уже не бас. дальше длина волны с диаметром диффузора вступают в
Не зря же ЭМОС ограничивают по частоте парой сотен Гц, дальше фигня-с

[_Сам_]

Бока Я лишь попытался разобраться в теоретической стороне вопроса. С практической инженерной точки зрения измерения Nota Bene для меня и так были убедительны, но оказывается, они убедительны не для всех. Некоторые продолжают упираться и спорить

[Бока]

_Сам_, я оказался владельцем целой коллекции роскошных пьезо датчиков для измерения вибрации, теперь душа горит в ожидании макета измерителя вибраций стенок колонки, выведенного на Спектралаб. То-то многое раскроется, ранее невидимое и неведомое.
ПС. Упорство некоторых - да не будет вам помехой на пути познания Истины.

[Sergo_PnL]

Скорость - это частота, ускорение - давление.

[Nota Bene]

де видно, что с 1 кГц акселерометр даёт завышенное значение относительно измерений микрофона.

Выше этой частоты заканчивается поршневой диапазон работы диффузора, и он переходит в режим зонного излучения (некоторые части диффузора двигаются в разных направлениях), поэтому так различаются АЧХ датчика и микрофона. Без ИМХО.

[Игорь Гапонов]

...

1. Хотя поршень и невесом, но из-за взаимодействия со средой к нему приходится прикладывать конечную силу F(t) = dx/dt * z_R, где z_R - комплексное сопротивление излучению.

...

2. Представим сопротивление излучению в виде z_R = ρ*с*S*( r_R + i * x_R ), где ρ - плотность среды, с - скорость звука, S - площадь поршня, а r_R и x_R безразмерные коэффициенты активного и реактивного сопротивления.

...

1. Т.е. сила пропорциональна не только производной, но и импедансу. Т.е. без учёта импеданса рассмотрение не корректно. Например, если импеданс обратно пропорционален частоте (чистая гибкость) получим частотнонезависимую силу, которая не имеет сдвига фазы со скоростью и пропорциональна ей, скорости, до частотнонезависимой константы. Так на НЧ работают наушники (при полной герметичности), причём, практически не излучая энергию (очень мала акт. составляющая), но оооочень громко .

2. Самое интересное, что учёт порядка осцилятора (например, пульсирующая сфера, диполь) позволяет использовать "нормальные" частотно независимые RCL элементы в модели нагрузки. В данном случае нагрузке малого поршня средой учитывается нулевой порядок. И нагрузка представляется в виде параллельно соединённых частотно независимых соколеблющейся массы m и активных потерь на излучение r: r*[jwtau/(1+jwtau)]; tau=m/r (с точностью до частотно независимых параметров среды). Собственно, ничего "физически" не меняется (из этой формулы можно получить "классику" и наоборот, и Ваши/не Ваши "выводы", приведённые здесь, совершенно не пострадают). Но теперь можно обычный электротехнический расчёт применять без опасности большой ошибки в "переходной зоне" (когда, поршень уже сравним с длиной волны, но колеблется как единое целое).

3. На самом деле, вопрос: какой датчик поля лучше: смещения, скорости или ускорения; упирается в точность и ограничения линейной коррекции (и механической и электрической!!!) электрического сигнала с него. Например, "конденсаторные" микрофоны на самом деле датчики смещения, подвергающегося механической линейной коррекции на подвижке (приблизительно дважды дифференцирующая цепь на частотах от нуля до резонанса, чем ниже частота сигнала относительно резонанса, тем точнее), которая делает смещение частотно независимым. Но с вытекающими последствиями: высокое напряжение поляризации из-за малого смещения, иначе коррекция на НЧ утонет в шумах (в электретах тоже порядка 20-100В потенциал поляризации), высокое натяжение мембраны и его стабильность, малые масса и смещения мембраны (последнее - НИ).

[SilentS]

На вопрос "скорость или ускорение" ответить очень просто, не прибегая ни к каким сложным формулам.

Известно, что динамик - электроакустический преобразователь, т.е. преобразует электрическую энергию в акустическую. В линейном режиме (т.е. когда гармоники меньше основного тона; поршневой или не поршневой здесь не имеет значения) выходная акустическая мощность линейно связана с входной электрической.
Далее, какие величины задают потребляемую электрическую мощность? Это квадрат тока на сопротивление. А как ток связан с механическими величинами? Ток создает силу, т.е. ускорение диффузора. Соответственно, получаем, что излучаемая акустическая мощность пропорциональна квадрату ускорения.

Ну и напротив, скорость просто не соответствует никакой электрической величине, поэтому она и не может создавать акустическое давление.

[Игорь Гапонов]

"Понравилось", особенно вот эти два противоречивых тезиса:

На вопрос "скорость или ускорение" ответить очень просто, не прибегая ни к каким сложным формулам.

/////

Ну и напротив, скорость просто не соответствует никакой электрической величине, поэтому она и не может создавать акустическое давление.

[Ka4aN]

Offтопик:

"Понравилось", особенно вот эти два противоречивых тезиса:

Неформальная логика, она такая. А вообще, уважаю людей, которые чтут закон сохранения энергии

[Sergo_PnL]

Одной скорости недостаточно для описания функции, это может быть как одно сочетание частоты и амплитуды, так и другое. Надо принимать в расчет ускорение и торможение.

[alexkh2008]

Допустим, динамик отрабатывает эл. сигнал по ускорению. Тогда, по прекращении сигнала с усилителя динамик не должен тут же останавливаться, он всего лишь должен перестать испытывать ускорение и двигаться равномерно?

[Игорь Гапонов]

Допустим, динамик отрабатывает эл. сигнал по ускорению. Тогда, по прекращении сигнала с усилителя динамик не должен тут же останавливаться, он всего лишь должен перестать испытывать ускорение и двигаться равномерно?

1. Хорошо, допустим.

2. Процесс "прекращения сигнала" тоже имеет ускорение, т.к. набранная до того скорость изменяется во времени . Но можно представить, что динамик до того не двигался (бесконечное торможение= КЗ по механике), тогда и мех.ускорения не будет. Т.е. без импеданса, который в линейной системе не зависит от НАЛИЧИЯ (мощности) возбуждения никуда

P.S. Я ещё раз приаттачу статейку с корректной экв. схемой ЭД ГГ (в ЗЯ или в БЭ). На рис. 19 показана ветвь, отражающая на НЧ нагрузку диффузора (апертуры) воздухом R_EL+C_EL. Напряжение на этой ветви эквивалентно скорости этой апертуры с прилегающим слоем воздуха, а ток через эту ветвь эквивалентен силе, действующей на этот слой воздуха. Все амплитуды и сдвиги фаз токов и напряжений на элементах полностью характеризуют и движение и электрические режимы элементов ГГ в рамках модели (с точностью до допущений и приближений) с электрической стороны преобразователя. Из модели в частности видно, что для источников в виде "самих по себе точных" ИН или ИТ мгновенно ни скорость, ни сила на апертуре поменяться не могут. Видны так же влияния возможных нелинейностей в элементах схемы. Например, что влияние НИ гибкости подвеса L_EM на ветвь апертуры невозможно исправить ни итуном ни инуном, но можно охватом этой ветви ОС ("истинная" ЭМОС) .

[SilentS]

Допустим, динамик отрабатывает эл. сигнал по ускорению. Тогда, по прекращении сигнала с усилителя динамик не должен тут же останавливаться, он всего лишь должен перестать испытывать ускорение и двигаться равномерно?

Дело в том, что усилители на НЧ, как правило, работают в режиме источника напряжения, а не тока. Поэтому под "прекращением сигнала" нужно понимать именно ноль напряжения, а не тока.
Так вот, ток мгновенно не исчезнет и по мере своего затухания будет создавать противо-эдс, ускоряя и тормозя диффузор даже после снятия напряжения. Во-вторых, на диффузор конечно же еще будет действовать упругая сила подвеса. (Вообще все эти процессы учитываются в комплексной кривой зависимости импеданса от частоты). В итоге, после снятия напряжения, диффузор еще может слегка поколебаться туда-сюда, в зависимости от полной величины добротности затихнет быстро или не очень. Но пока он тормозиться - будет излучать.

Мои простые соображения, связывающие мощность - ток - ускорение - акустическая мощность работают только для стационарного процесса (жаль, что Игорь Гапонов этого не понял). Нестационарные процессы сложнее анализировать таким образом, но в принципе тоже можно показать с помощью (например, подавая дельта импульсы на вход разной длительности и интенсивности и смотреть что на выходе), что звуковое давление пропорционально ускорению, а мощность - ускорению в квадрате.

[shap2770]

Какие ускорения?Какие замедления?фигня!
Нужна чёткая пропорция перемещение дифузора относительно напряжения входного сигнала и всё!!!
Все эти ЭМОСы и АОСы сольют обычному оптическому датчику,ну типа натяжителя ленты,как на бобинниках ,
между лампой и фоторезистором лёгкая оптическая клин-полоска приклеенная на дифузор,линейно перекрывающая
свет.

[Nota Bene]

что звуковое давление пропорционально ускорению в квадрате.

излучаемая акустическая мощность пропорциональна квадрату ускорения.

Так, я не понял, мощность или давление (SPL) ??? Вы уж определитесь

Нужна чёткая пропорция перемещение дифузора относительно напряжения входного сигнала и всё!!!

Offтопик:
О сколько нам открытий чудных готовит просвященья дух....

[Игорь Гапонов]

...
Мои простые соображения, связывающие мощность - ток - ускорение - акустическая мощность работают только для стационарного процесса (жаль, что Игорь Гапонов этого не понял). Нестационарные процессы сложнее анализировать таким образом, но в принципе тоже можно показать с помощью (например, подавая дельта импульсы на вход разной длительности и интенсивности и смотреть что на выходе), что звуковое давление пропорционально ускорению в квадрате.

Я то понял. Те "упрощения математики", о которых Вы говорите, сразу приведены ТС в ссылках и рассуждениях первого поста. Там же указано (правда в формуле ), что объёмная скорость таки создаёт давление при ненулевых импедансах объекта воздействия (среды), а давление создаёт скорость при небесконечных импедансах.

Так же нередки случаи, когда именно для слуховых ощущений ("аудио" - то чем мы занимаемся) излучаемая мощность совершенно не играет роли. Например, прослушивание АС в закрытом помещении или в ближней зоне, или "наушники".

Это корректно, но не Ваши тезисы про "не прибегая к сложным формулам" и "скорость не соответствует никакой эл. величине ".

Вам надо сделать следующий шаг: поверить/проверить, что схема и мат. уравнение есть интерпретации одной и той же модели/представления, которая описывает любые сигналы и процессы (включая переходные, которые Вы называете ошибочно "нестационарными") возможные в её рамках.

[alexkh2008]

... Из модели в частности видно, что для источников в виде "самих по себе точных" ИН или ИТ мгновенно ни скорость, ни сила на апертуре поменяться не могут. Видны так же влияния возможных нелинейностей в элементах схемы. Например, что влияние НИ гибкости подвеса L_EM на ветвь апертуры невозможно исправить ни итуном ни инуном, но можно охватом этой ветви ОС ("истинная" ЭМОС) .

Нам, по идее, не нужно получать не неискаженное напряжение, не неискаженный ток усилителя, пусть с нулевым выходным сопротивлением или еще с каким-либо, а нужно - неискаженное усилие, прикладываемое к диффузору. КАК?

[Игорь Гапонов]

Нам, по идее, не нужно получать не неискаженное напряжение, не неискаженный ток усилителя, пусть с нулевым выходным сопротивлением или еще с каким-либо, а нужно - неискаженное усилие, прикладываемое к диффузору. КАК?

Правильно! С поправкой: нескажённую силу (или скорость, т.к. воздух очень линейная среда и линейная коррекция скорость/давление, в общем-то, не представляет трудности) к слою воздуха, прилегающего к апертуре (это, чтоб все типы оформления, включая рупор, объять )

[_Сам_]

заканчивается поршневой диапазон работы диффузора

возможно и так. Но из приведённых формул в первом посте следует, что даже если мы волшебники, которые сделали идеальный поршень и начали колебать его с постоянной амплитудой, но разной частотой, то начиная с некоторой частоты скорость нарастания давления от частоты замедлится. Квадратичная функция превратится в линейную. Таким образом, если мы захотим сделать ЭМОС для СЧ, то придётся следить, чтобы диаметр СЧ динамика был не слишком большим. Иначе даже идеальный акселерометр будет врать.

Допустим, динамик отрабатывает эл. сигнал по ускорению. Тогда, по прекращении сигнала с усилителя динамик не должен тут же останавливаться, он всего лишь должен перестать испытывать ускорение и двигаться равномерно?

вспоминаем 2-й закон Ньютона. ma = F₁+F₂+F₃+... Масса на ускорение диффузора равна сумме сил действующих на него. На диффузор динамика действует много сил кроме силы Ампера. (упругость подвеса, трение подвеса, разница давлений между передней и задней стороной диффузора). Даже если разорвать электрическую цепь катушки и устранить электромагнитную силу, то динамик мгновенно не остановится, а начнёт совершать затухающие колебания под действием оставшихся сил.